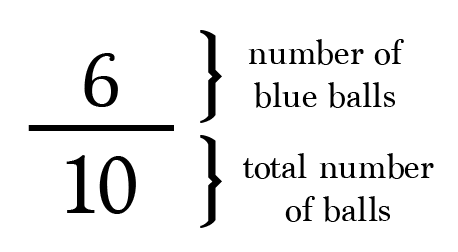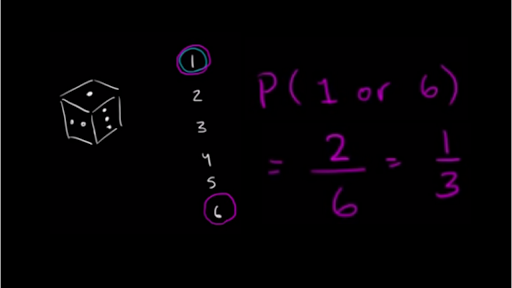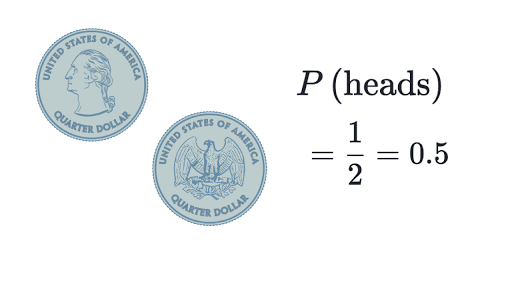Probability Infinite Marbles Chance Of Getting Exactly Three

If we got a blue marble before then the chance of a blue marble.

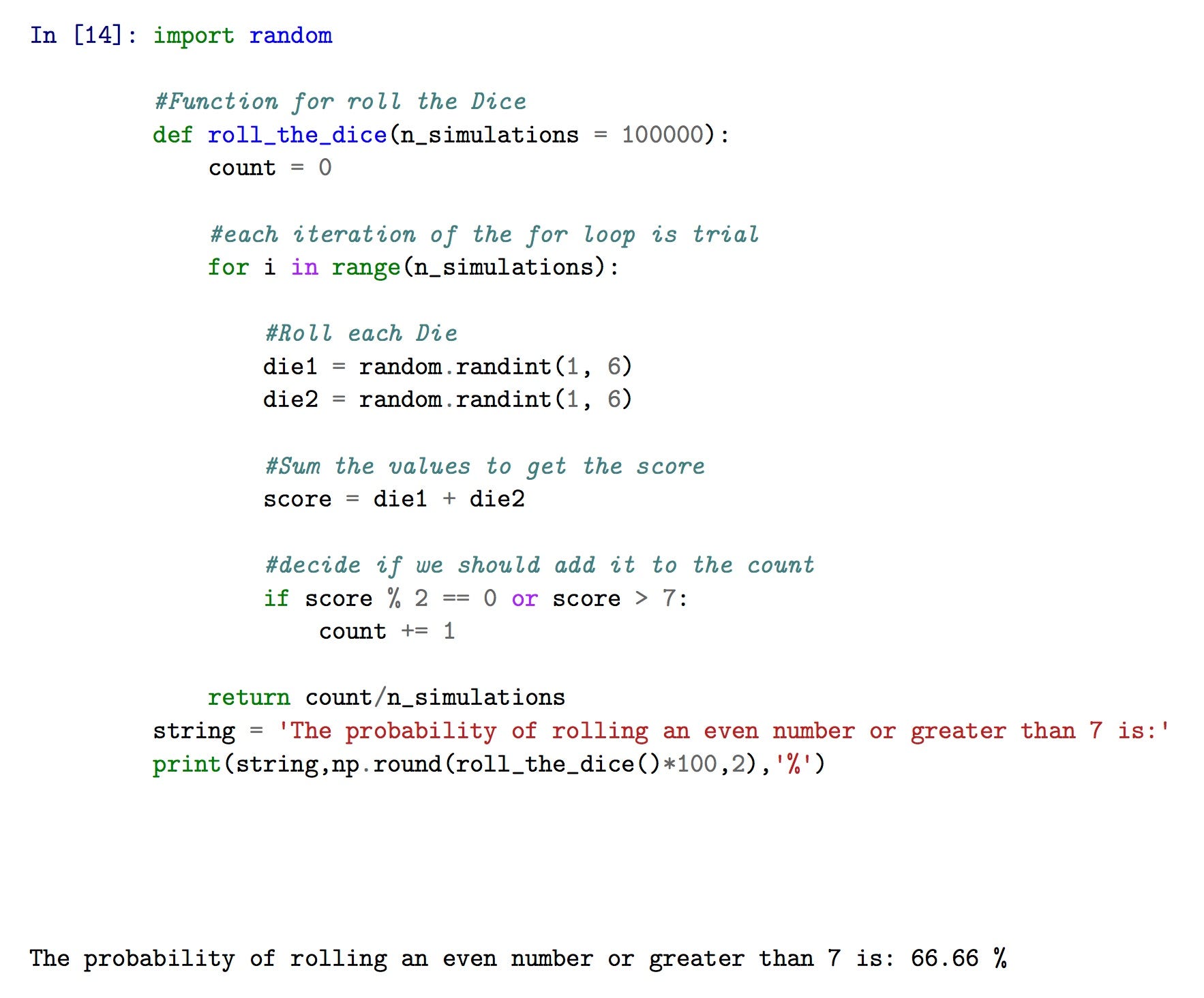
Probability infinite marbles chance of getting exactly three. Given that it is red there now remain 19 marbles in the bag of which 4 are red. Probability examples a jar contains 30 red marbles 12 yellow marbles 8 green marbles and 5 blue marbles what is the probability that you draw and replace marbles 3 times and you get no red marbles. All of the outcomes must add up to 1. A hypergeometric distribution is used in situations where the sampling is done from an infinite population and the successive outcomes are independent.

A draw the tree diagram for the experiment. So the probability of getting a blue is 1 3. Suppose there are 15 black and 12 red marbles in an urn. Therefore the probability of getting a red on the second draw 4 19.

Given that it is a red there now remain 18 marbles in the bag and 3 are red. You reach in and randomly select 8. The probability that the third is red 3 18. B find probabilities for p bb p br p rb p ww p at least one red p exactly one red 3.

Therefore the probability of not drawing a red marble is the same as one minus the probability of drawing a red marble. The binomial probability calculator will calculate a probability based on the binomial probability formula. Trials n must be a whole number greater than 0. When the probability of one event depends on another the events are dependent.

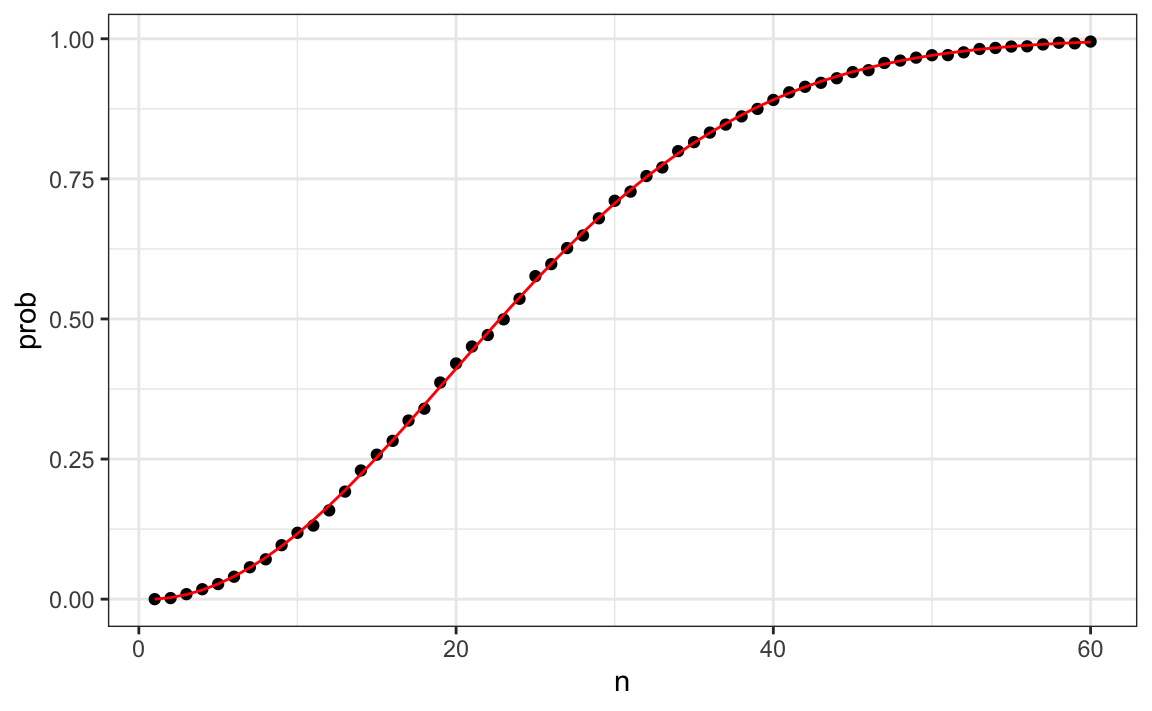
What are the chances of getting a blue marble. What is the probability of getting exactly 3 heads out of 10 tossing experiments 1172. You will also get a step by step solution to follow. There are 55 marbles 25 of which are not red p getting a color other than red p 25 55 455 probability of this happening 3 times in a row is.

There are a total of 3 4 2 9 marbles in the box. Probability to get heads 4 1 0 25 100 56 0 56 1000 510 0 510 10000 4988 0 4988 notice that for 10000 flip the probability is close to 0 5 try the same experiment to get the coin toss probability with the following coin flip simulation. The probability of getting a red with the first draw is therefore 5 20. The chance is 2 in 5.

But after taking one out the chances change. This is the number of times the event will occur. Marbles in a bag. However if the first ball was red there will be 1 red and 2 blue balls left so the probability the second ball is blue is 2 3.

Two marbles are drawn without replacement from a jar containing 4 black and 6 white marbles. After you have flipped the coin so many times you should get answers close to 0 5 for both heads and tails. Two marbles are drawn without replacement. 2 blue and 3 red marbles are in a bag.

A jar contains 4 black marbles and 3 red marbles. If we got a red marble before then the chance of a blue marble next is 2 in 4.