Prove The Serpinski Carpet Is Connected

Condition b in definition 2 3 is not only essential for our proof to work but necessary and sufficient for a generalized sierpiński carpet to be connected thanks to theorem 2 in 8 while.

Prove the serpinski carpet is connected. The construction of the sierpinski carpet begins with a square. We prove a uniform harnack inequality for positive harmonic functions. Mosco convergence is not straightforward to prove on the sierpinski carpet graph although we will present an argument in this section. The sierpinski curve is a base motif fractal where the base is a square.

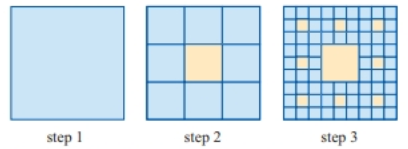
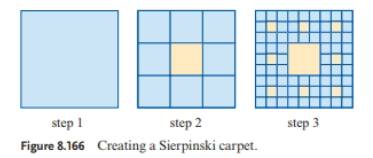
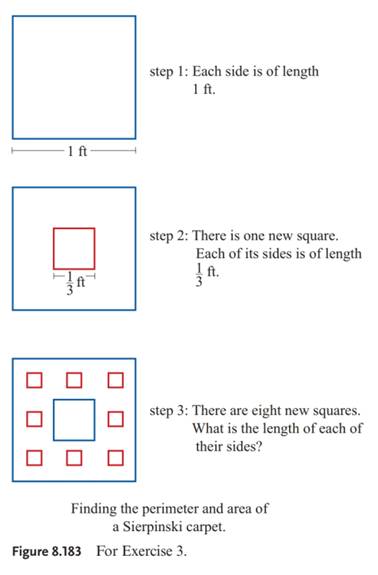
The technique of subdividing a shape into smaller copies of itself removing one or more copies and continuing recursively can be extended to other shapes. The sierpiński carpet is a plane fractal first described by wacław sierpiński in 1916. The curve is also known as the sierpinski universal plane curve sierpinski square or the sierpinski carpet. The carpet is one generalization of the cantor set to two dimensions.

The technique of subdividing a shape into smaller copies of itself removing one or more copies and continuing recursively can be extended to other shapes. It has named after the polish mathematician waclaw sierpinski 1882 1969 but it was stefan mazurkiewicz who found the curve in. Note that simply connected spaces are assumed to be connected and so we only consider connected topological. The main take away results are theorem 2 4 convergence of the green forms and lemma 2 8 consequences of theorem 2 4 suitably specialized to the.

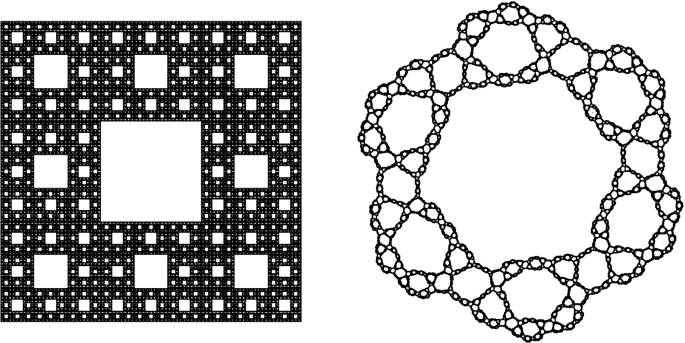
The sierpinski carpet is a plane fractal first described by wacław sierpiński in 1916. For these examples the proper connected parabolic limit sets are circles and hence have conformal dimension 1 while is homeomorphic to the sierpinski carpet and therefore has conformal dimension 1 by a result of j. Another is the cantor dust. In fact we prove that the cumulative degree distribution of our networks g t obey power law log 8 log 3 which is the hausdorff dimension of sierpinski carpet.

For instance subdividing an equilateral triangle. We consider a class of fractal subsets of rd formed in a manner analogous to the construction of the sierpinski carpet. And when can this subspace be chosen to be open. The carpet is one generalization of the cantor set to two dimensions.

I wonder how widespread this phenomenon is. To give an example even the resolvent convergence i e. The square is cut into 9 congruent subsquares in a 3 by 3 grid and the open central subsquare is removed. As the answer to this question indicates any manifold contains an open dense subset which is homeomorphic to mathbb r n and so for manifolds the stronger of the two properties holds.

Applying similar techniques in a simpli ed setting we. We also find the uniform positive lower bound of the average clustering coefficient of g t by using the self similarity c t 0 642 for all t and the limit lim t c. Theorem 1 1 therefore applies and has the clp.