Probability Colored Marbles With Replacement

Initially there is a 2 5 chance of picking a white marble.
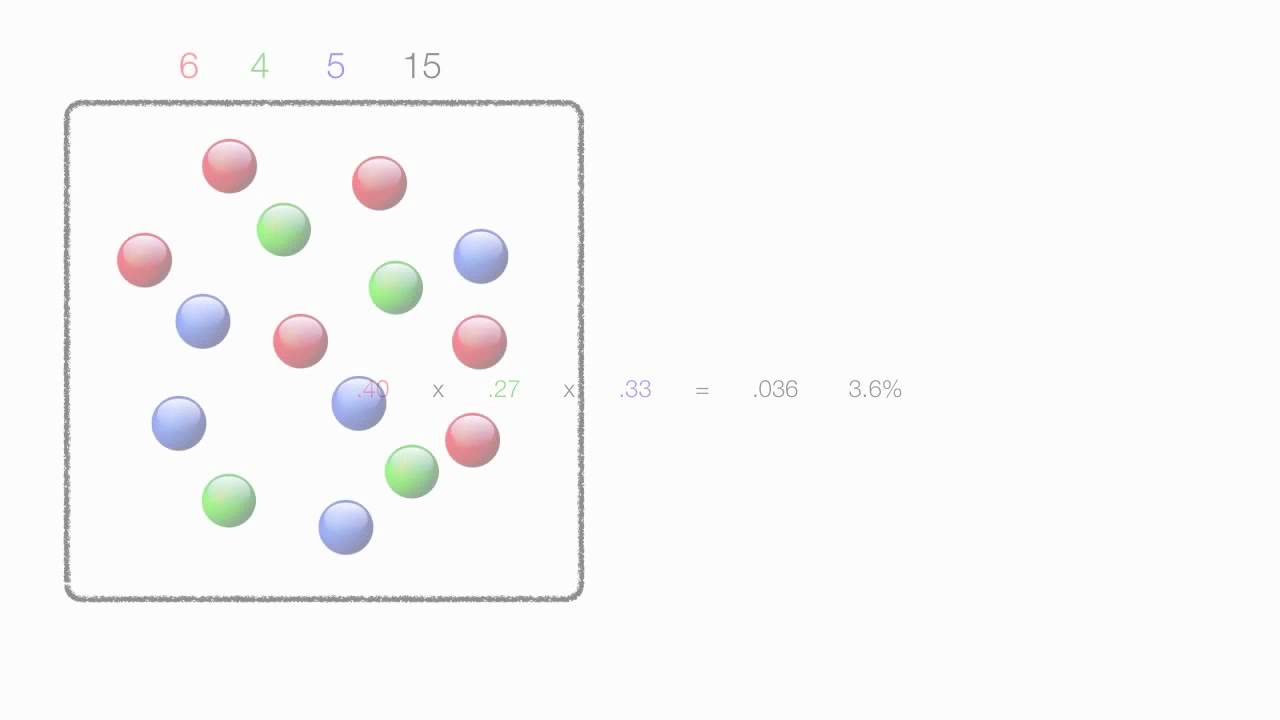
Probability colored marbles with replacement. This is called probability without replacement or dependent probability. A box contains 5 purple marbles 3 green marbles and 2 orange marbles. According to wikipedia in probability and statistics an urn problem is an idealized mental exercise in which some objects of real interest such as atoms people cars etc are represented as colored balls in an urn or other container like box. Ii one red and one blue.
And in our case. So they say the probability i ll just say p for probability. P b a is also called the conditional probability of b given a. Number and color of marbles in the bag replacement rule.
I at least one blue. And so this is sometimes the event in question right over here is picking the yellow marble. So the probability of getting 2 blue marbles is. The sample space for the second event is then 19 marbles instead of 20 marbles.
The probability of picking a yellow marble. Iii two of the same color. One example uses with replacement and one example uses without replacement. On your second pull since we are not replacing marbles there s a 3 4 chance that you pick a b.
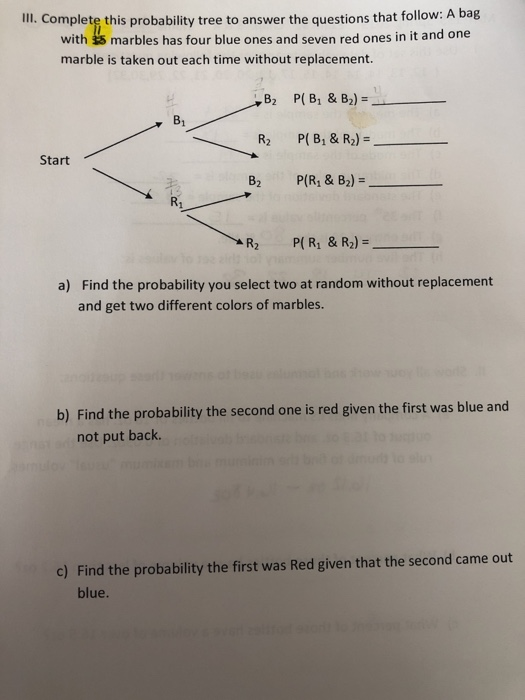
Alice chooses 2 marbles without replacement and then bob chooses 2 marbles. Let s break it down into cases. A show all the possible outcomes using a probability tree diagram. And we write it as probability of event a and event b equals the probability of event a times the probability of event b given event a let s do the next example using only notation.
A a probability tree diagram to show all the possible outcomes. This video goes through 2 examples of probability. When you start learning probability and statistics you can often find problems with probability urn. You pick a white marble followed by a blue marble.
Find the probability of pulling a yellow marble from a bag with 3 yellow 2 red 2 green and 1 blue i m assuming marbles. The probability for drawing two marbles of red color without replacement by using the formula. B calculate the probability of getting.